[알고리즘 이론] DFS와 BFS

* DFS와 BFS 이해 전 그래프에 대한 이론을 알고 있다면 도움이 될 것이다. 

 

 

DFS 

깊이 우선 탐색(Depth-First Seartch)는 그래프 완전 탐색 기법 중 하나이다. 

DFS는 그래프의 시작 노드부터 시작하여 탐색할 분기를 정하고, 끝까지 탐색 후 다음 분기로 넘어가서 다시 탐색하여 모두 다 탐색하는 알고리즘이다. 

 

출처 - 위키피디아(https://en.wikipedia.org/wiki/Depth-first_search)

 

DFS는 Stack 또는 재귀함수를 이용하여 구현할 수 있으며 시간 복잡도는 O(노드 수 + 에지 수)이다. 

재귀함수를 사용할떈 스택 오버플로를 조심하며 사용해야한다. 

 

 

우선 이런 그래프가 있다고 가정해보자.

 

이 그래프를 인접 리스트로 표현한다면 아래처럼 표현 할 수 있다. 

 

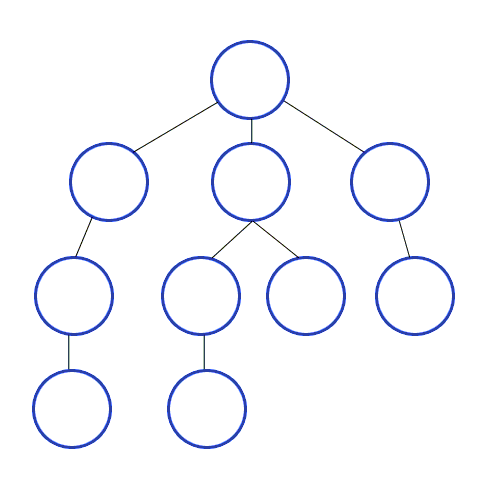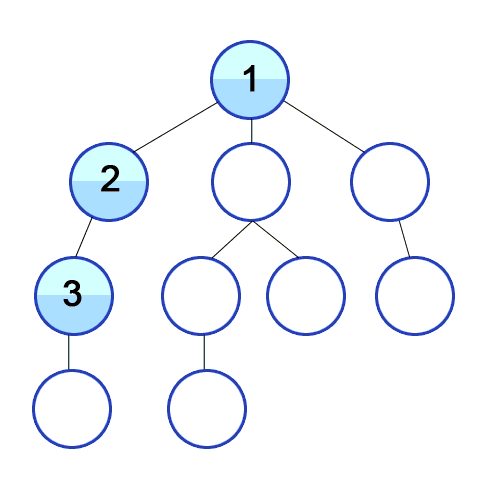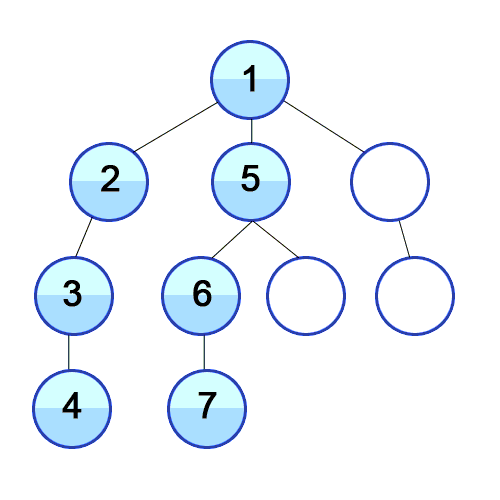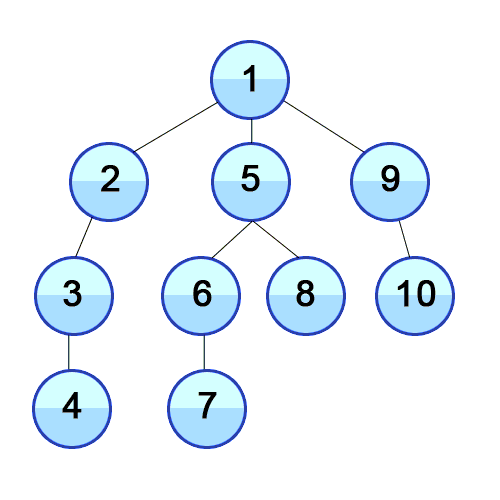
1) 1부터 시작한다고 가정하고 1을 Stack에 넣음과 동시에 1이 들어 왔다는 것을 체크해준다.

 

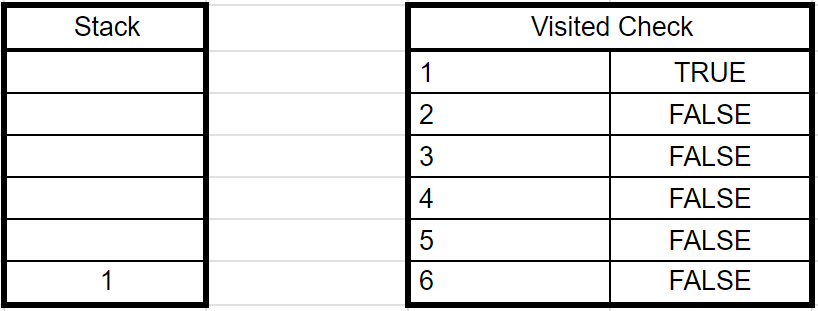
2) 1을 Stack에서 뺴주고 1과 연결 되어 있는 2와 4를 Stack에 넣어주고, 들어왔다는 것을 체크 해준다.

 

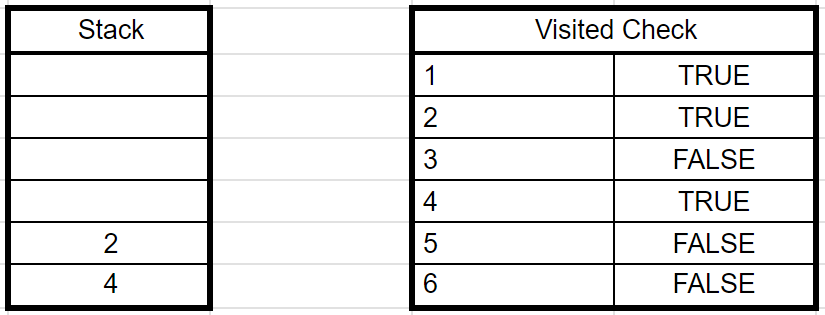
3) Stack 맨 위에 있는 2를 빼주고, 연결 되어있는 3을 Stack에 넣고 들어왔다는 것을 표시한다.

 

4) Stack 맨위에 있는 3을 뺴주고 연결된 2와 6을 넣어주어야 하지만 2는 이미 확인이 된 노드이기 때문에 6만 넣어준다.

 

5) Stack 맨 위에 있는 6을 빼준다. 여기서 연결된 노드가 없거나 모두 들어 갔다왔다면 넣어주지 않는다.

 

7) 이 과정을 반복하고, 모든 노드에 방문 했다면 종료한다. 

 

 

DFS을 재귀함수로 구현한 코드는 다음과 같다.

#include <iostream>
#include <vector>

static vector<vector<int>> A;
static vector<bool> visited;

void DFS(int v)
{
    if (visited[v])
        return;

    visited[v] = true;

    for (int i : A[v])
    	DFS(i);
}

 

 

---

 

 

 

BFS

너비 우선 탐색 (Breadth-First Search)는 그래프 완전 탐색 기법 중 하나이다. 

BFS는 DFS와 다르게 출발점을 잡고 출발점에서 가까운 노드를 방문하며 탐색하는 알고리즘이다. 

출처 - 위키피디아(https://en.wikipedia.org/wiki/Breadth-first_search)

 

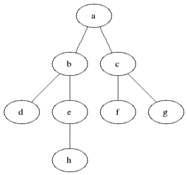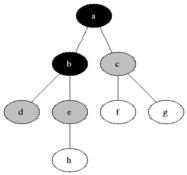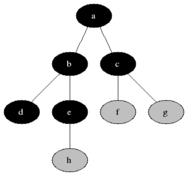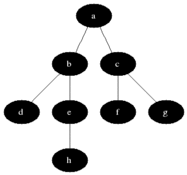
BFS는 Queue를 이용하여 구현할 수 있으며 시간 복잡도는 O(노드 수 + 예지 수)d이다. 

너비 우선 탐색은 시작 노드와 가까운 노드부터 탐색하므로 목표로 도착하는 경로가 여러개일때 최단 경로를 보장합니다. (EX. 미로)

 

예시는 위와 같은 그래프를 사용하도록 하겠습니다.

 

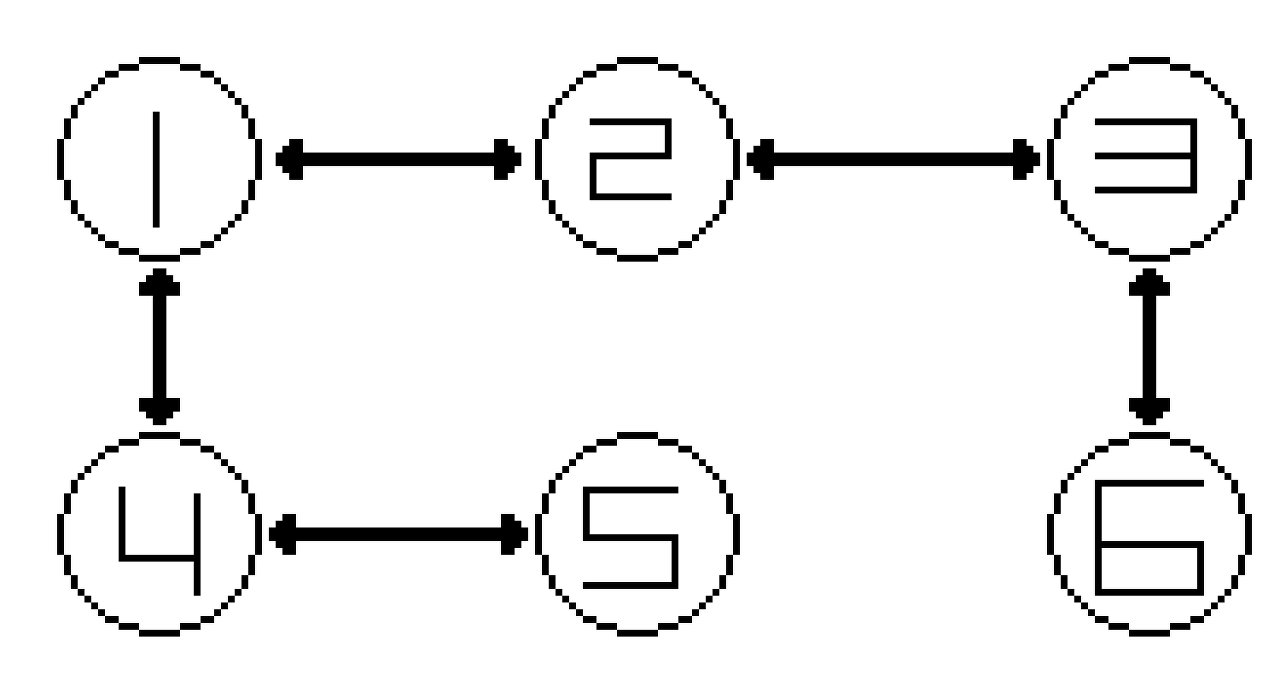
인접리스트로 표현한다면 이와 같다. 

 

1) 우선 시작점을 Queue에 넣어주고, 들어왔었다는 것을 체크해준다.

 

2) Queue에서 1을 빼주고, 1과 연결된 노드들을 Queue에 넣어주며, 들어온 것을 체크해준다.

 

3) Queue에서 2를 빼주고 연결된 노드를 모두 넣어주며 들어온 것을 체크한다.

4) Queue에서 4를 빼준다. 이후 연결된 노드인 1과 5를 넣어줘야 하지만 1을 들어온 적이 있기에 5만 넣어준다.

 

5) 이러한 작업을 계속 하다보면 모든 노드에 들리고, Queue가 비게 될텐데 그때가 탐색이 끝난 상황이다.

 

 

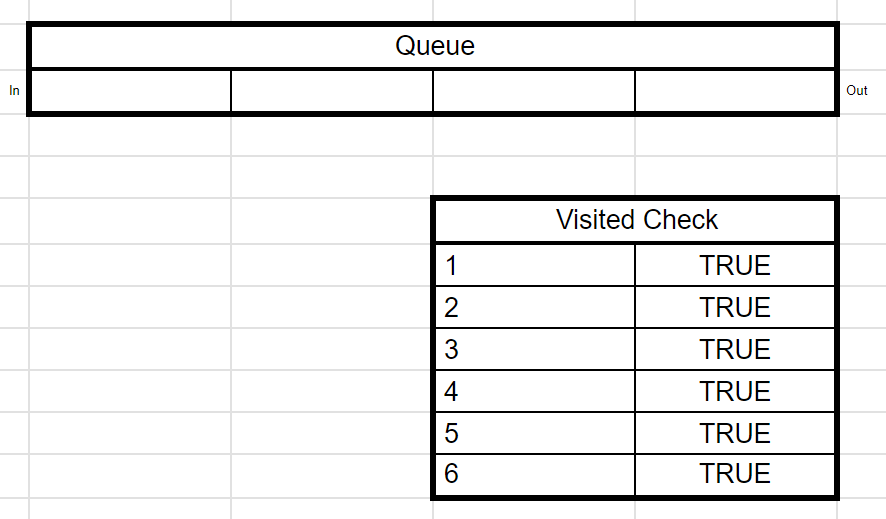
BFS를 구현하면 다음과 같다.

#include <iostream>
#include <queue>

vector<vector<int>> graph;
vector<bool> visited;

void BFS(int index)
{
    queue<int> que;
    que.push(index);
    visited[index] = true;

    while (!que.empty())
    {
        int current = que.front();
        que.pop();

        for (int i : graph[current])
        {
            if (visited[i])
                continue;
            visited[i] = true;
            que.push(i);
        }
    }
}